The Critical Strike Algorithm Revisited
Justin D. — September 20, 2020
Overview
In League of Legends, critical strikes are basic attacks that deal double damage. From our last look into critical strikes, we know that Riot’s critical strike algorithm features “crit smoothing,” so while the occurrence of crits is still random, players are less likely to get lucky or unlucky streaks of crits or non-crits. In other words, crit rates fluctuate from attack to attack. By gaining an understanding of how crit rates change based on previous attacks, players can gain a competitive edge in knowing if their critical strike chance has increased or decreased.
Introduction
The data we’re using comes from the same transformed footage of basic attacks in the practice tool that was used in our previous study on crits. Our dataset consists of 2,700 attacks at each tenth crit rate from 10% to 90% with each attack being either a 1 or 0 which represent a crit or non-crit, respectively. In order to gain insight as to how crit chance is altered based on whether or not previous attacks were crits or non-crits, we’ll compare two datasets:
- The actual data that we observed in our videos of League in the practice tool.
- Simulated data where attacks are completely independent, meaning that each attack’s chance of being a critical strike doesn’t depend on the attacks that came before it.
By comparing the behavior between the observed in-game attacks and the simulated attacks, we can see how much League adjusts crit chances. To do this in a statistically sound way, we will use a method called hypothesis testing. In hypothesis testing, we start with a null hypothesis that we assume to be true, unless presented with evidence that says otherwise. For our problem, the null hypothesis is that critical strikes are independent on every attack. (Remember: this means that the crit rate of your next attack is the same regardless of whether your last attack was a crit or non-crit.) We also have an alternative hypothesis that is merely the contrary to the null hypothesis: critical strikes are not independent on every attack. This means that the crit rate of your next attack is different if your last attack was a crit or non-crit.
Methods
Previously, Doran’s Lab established (with a high degree of certainty) that attacks are not independent and that the crit chance of your next attack depends on whether your last attack was a crit or non-crit. However, knowing this is not particularly useful. What would be more useful is determining how crit rates are affected by different sequences of attacks. Then, we could give players rules for when their crit chance is higher or lower than their listed crit chance in-game.
To investigate, we took every unique sequence of three attacks and computed the crit rate after each of these sequences. The crit rate of a sequence is calculated by taking the number of times a crit happened after the sequence and dividing it by the number of times that the sequence appeared in our data. Below are the results of our calculations:
In the above tables, we see how many times a sequence appeared, how many times there was a crit after the sequence, and the crit rate computed from dividing those two numbers. This lets us easily see how crit rates fluctuate in-game depending on the attacks that came before it. However, we can’t rush to conclusions from our data just yet. It’s important to understand that our observed crit rates could have occurred due to random chance, even if there was no crit smoothing. Because of this caveat, we’ll need evidence that shows that observing crit rates like the ones we observed could not have occurred by random chance if we want to recommend crit rules to players. This is where our null hypothesis comes into play.
First, we’ll generate attacks that are independent using Python scripts so we can compare them to the actual observed data. When we collected our data, we observed every tenth crit rate over 2,700 attacks, so we will randomly generate 2,700 attacks at whatever crit rate of the data that we want to study. From these simulated attacks, we can observe what the crit rates should be for each attack sequence if attacks were independent. Because the process of generating attacks is random, we’ll want to figure out the range or distribution of crit rates that each sequence can take on. Then, we’ll want to see where the crit rate for a sequence of attacks from our data falls in the distribution. Doing so will look like this:

Attack Sequence [0, 1, 0] at 80% Crit Rate. (Note: A 0 and 1 correspond to a non-crit and crit, respectively.)
By figuring out where the data crit rate falls for a particular sequence, we can compute it’s percentile - in other words, the percentage of generated crit rates that fall below our data crit rate. If the observed percentile falls outside of the 5th or 95th percentile, we have evidence of how Riot’s crit algorithm operates because it would be odd to observe a crit rate that high or that low for that particular sequence if crits are generated independently. If this is the case, we can reject our null hypothesis and can claim (with confidence) that crits are not generated independently for that particular attack sequence.
Results
The tables below are the results of our analysis. The index of the table represents the sequence of attacks we are observing. Note that Random will refer to any data from our simulated attacks while Data refers to our observed attacks. With that in mind, Random Crit % represents the average number of times a 1 (crit) appeared after that particular sequence divided by the average number of times that sequence appeared (Rnd Counts) in our simulated data. Data Crit % represents the number of times a 1 (crit) appeared after that particular sequence divided by the number of times that sequence appeared (Data Counts) in our observed data. Note: Rnd Counts and Data Counts do not count the sequence if the last attack of the sequence is the final attack in our dataset. Crit% Diff takes the Data Crit % column minus the Random Crit % column. PCTL of DataCrit describes the percentage of generated crit rates that fall below our data crit rate. The last two columns describe the 5th and 95th percentiles of the randomly generated attack crit rates, respectively.
Discussion
By examining the tables (specifically the PCTL of Data Crit column), we observe large amounts of crit smoothing occuring at the 30, 60, and 70% crit rates. Keep in mind that a percentile above the 95th percentile or below the 5th percentile does not guarantee a crit or a non-crit if that sequence were to be observed in-game. Rather, we have evidence that supports the claim that the crit strike algorithm has some dependence on that particular sequence of that crit rate when generating crits or non-crits. However, it may be useful for players to track the sequences of their attacks and, depending on their crit strike chance, use that information to judge the likelihood that they will crit or not crit on their next attack which can provide a calculated edge in engagements or assassinations.
There are two other interesting takeaways from the tables. Examining the table "Crit Chance: 60%," the data crit rates for the sequences [0, 0, 0] and [1, 1, 1] are 48% and 68%, respectively. Here, the crit algorithm is smoothing the crit rate, but in an unexpected way. Rather than boosting the [0, 0, 0] sequence up, the crit rate is being pulled down. Conversely, the [1, 1, 1] sequence is being boosted up. Depending on the sequence, the smoothing that’s occurring could lead to crit or non-crit streaks which is a hidden crit rate buff/debuff. The other takeaway comes from the data counts column. From the table "Crit Chance: 30%," we can see the sequence [1, 1, 1] appeared 34 times and had a crit rate of 23%. This crit rate was deemed as significant by our test and the large drop in crit rate is due to the crit algorithm not wanting the player to crit three times in a row when only at 30% crit rate which leads to the low number of times that the sequence appeared.
Future Research
Due to us only observing crit rates at every tenth percent, we fail to observe the extent of crit smoothing that may be occuring at every fifth percent. In future experimentation, we should sample from at least the 25% and 75% crit rates as all items give 25% crit chance (with the exception of Cloak of Agility providing 20%). Then, we can study how the crit algorithm operates for champions who build 1 to 3 full crit chance items for the current meta. Additionally, because we used the same data from our previous study on crit smoothing, our work has the same limitations noted at the end of the previous article.
Note: Why did we only look at three attacks?
By observing the “optimal accuracy” of different rules for predicting crits, we decided to observe three attacks. Here’s how we computed the “optimal accuracy” of a prediction rule. A prediction rule is where we input some sequence of attacks and predict the next attack based on those attacks. For example, if we input the sequence [0, 0, 0] into our function, the next attack can be a crit or a non-crit. We know that with any attack sequence, there is no guarantee that you’ll crit or not crit. Because of this, we can’t create prediction rules that definitively say if an attack sequence will crit or not crit. However, we can try to see how close we can get to perfect predictions. What if we found if a crit or non-crit occurred most often after a sequence? Then, we’ll check and see how many times that actually happened. Going back to our example, if we say that [0,0,0] was generally followed by a crit, then we would want to see how many times that [0,0,0] was actually followed by a crit. By counting how many times we get a match and dividing that number by the total number of attack sequences from the data, we get our optimal accuracy. Similar to our operations with the crit rates, we’ll compute the optimal accuracy for randomly generated attacks multiple times and create a distribution of the optimal accuracies these randomly generated attacks can take on. We’re doing these same operations because we want to show how rare observing the optimal accuracy in attacks generated from Riot’s crit algorithm is when compared to attacks generated independently. Doing so will look like this:

Distribution of Random Optimal Accuracy From 3 Attacks at 50% Crit Rate
We can do these operations again, but this time looking at four attacks and five attacks:

Distribution of Random Optimal Accuracy From 4 Attacks at 50% Crit Rate
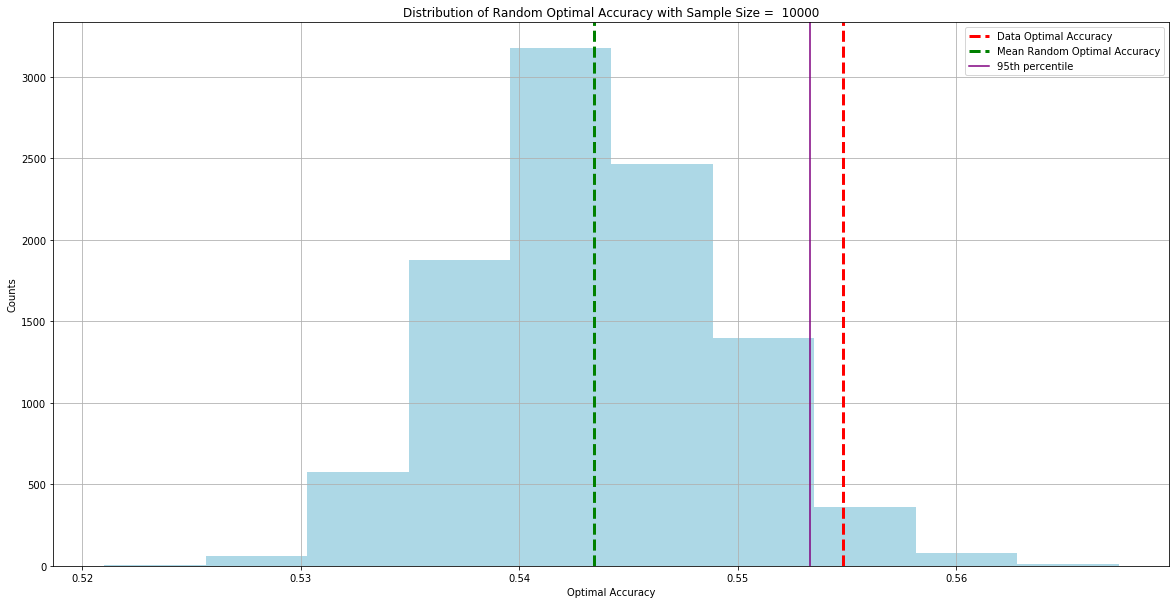
Distribution of Random Optimal Accuracy From 5 Attacks at 50% Crit Rate
Looking at the Data Optimal Accuracy line, we can see that the distance between it and the 95th percentile of the Random Optimal Accuracy gets smaller and smaller as we observe more attacks. Because three attacks had the largest gap between these two lines, we believe that looking at sequences of three attacks would have the most predictive power when trying to create crit rules. We did not consider sequences of one or two attacks due to the low number of unique attack sequences.
Join in on the fun!
At Doran's Lab, we strive to keep our process transparent and accessible. We've included the data corresponding to this article in a public Github repository for you to download and use.


